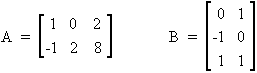
b) B × A
c) ½ B½
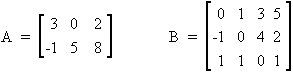
b) B × A
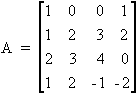
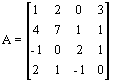
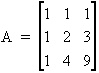
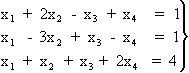
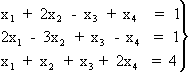
a)
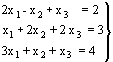
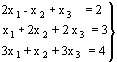
a) No es posible efectuar A+B pues se trata de dos matrices de distinto orden. La matriz A pertenece al conjunto de matrices de 2x3 (dos filas por tres columnas, M2x3), mientras que B pertenece al conjunto de matrices de 3x2. (M3x2 ). Para que dos matrices puedan sumarse deben ser del mismo orden, es decir, deben pertenecer al mismo conjunto de matrices. b) B × A
Como B Î M3x2 y A Î M2x3 , es posible efectuar el producto de la matriz de B por A, ya que el número de columnas de la matriz que pre-multiplica, B, coincide con el número de filas de la matriz que post-multiplica, A. El resultado será una matriz de 3x3. Se multiplican mediante el producto escalar los vectores fila de la matriz B por los vectores columna de la matriz A, colocando el escalar resultante como el elemento de la matriz producto correspondiente a la fila y columna multiplicadas. Es decir, el escalar resultante de multiplicar la segunda fila de B por la tercera columna de A, será el elemento a23 de la matriz B × A , (elemento de tercero de la segunda fila de B × A).
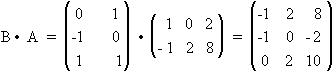
Como B es una matriz de 3x2 no tiene el mismo número de filas que de columnas, no puede plantearse calcular su determinante. Sólo está definido el determinante de una matriz para el caso de matrices cuadradas (mismo número de filas que de columnas).
2.-
a) A × B
Como A Î M2x3 y B ÎM3x4 , es posible efectuar el producto de la matriz de A por B, ya que el número de columnas de la matriz que pre-multiplica, A, coincide con el número de filas de la matriz que post-multiplica, B. El resultado será una matriz de 2x4. Se multiplican mediante el producto escalar de los vectores fila de la matriz A por los vectores columna de la matriz B, colocando el escalar resultante como el elemento de la matriz producto correspondiente a la fila y columna multiplicadas. Es decir, el escalar resultante de multiplicar la segunda fila de A por la tercera columna de B, será el elemento a23 de la matriz A × B , (elemento de tercero de la segunda fila de A×B).
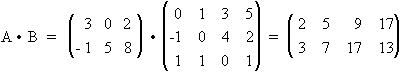
3.- Para resolver el determinante de la matriz A se puede emplear el método del desarrollo de un determinante por los elementos de una línea (o columna).
El determinante de una matriz A es igual a la suma de los productos de los elementos de una fila o columna por sus correspondientes adjuntos. El adjunto del elemento aij de una matriz cuadrada sería el determinante
Se podrían hacer operaciones entre filas o columnas de la matriz para que la fila o columna escogida contuviera el mayor número de ceros posible y, de esta manera, simplificar el número de adjuntos a calcular. Dada la matriz del ejercicio, prescindiendo de hacer esas operaciones entre filas o columnas, y desarrollando el determinante a partir de la primera fila queda :
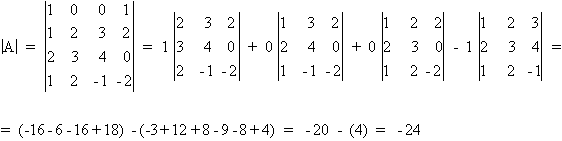
4.- Para resolver el determinante de la matriz A se puede emplear el método del desarrollo de un determinante por los elementos de una línea (o columna).
El determinante de una matriz A es igual a la suma de los productos de los elementos de una fila o columna por sus correspondientes adjuntos. El adjunto del elemento aij de una matriz cuadrada sería el determinante
Esta vez, se operará entre filas o columnas de la matriz para que la fila o columna escogida contenga el mayor número de ceros posible, y de esta manera se reducirá el número de adjuntos a calcular. Dada la matriz del ejercicio, a la segunda columna se le va a restar la primera multiplicada por dos y a la cuarta columna se le va a restar la primera multiplicada por tres. La matriz resultante tiene el mismo determinante que la matriz original, pero con la ventaja de que el determinante de orden 4 se va a reducir a resolver un determinante en lugar de 4 de orden 3. Así se tiene que:
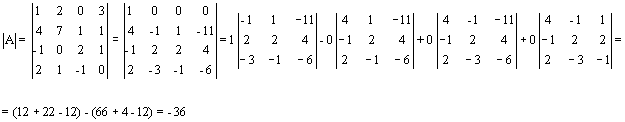
5.- Para saber si la matriz A admite inversa se calcula el determinante de A, pues en el caso de valer 0, la matriz A no admitirá inversa.
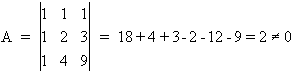
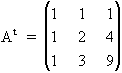
La matriz adjunta de la traspuesta de A es :

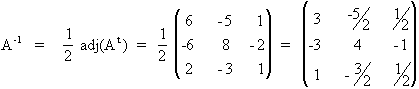
6.- Discutir un sistema consiste en determinar si tiene o no solución, es decir, si es compatible o incompatible, y en el caso de que tenga solución, determinar si ésta es única (sist. compatible determinado) o si tiene infinitas soluciones (sist. compatible indeterminado). El Teorema de Rouché-Frobenius permite saber si el sistema tiene o no solución y, si la tiene, si es única o existen infinitas soluciones. El Teorema se basa en la comparación de los rangos de la matriz A (matriz de coeficientes del sistema de ecuaciones), y la matriz A* (matriz de coeficientes del sistema ampliada con el vector columna de términos independientes del mismo).
Teorema
Dado un sistema de ecuaciones lineales:
- rg(A) < rg(A*) Þ sistema incompatible
rg(A) = rg(A*) = nº incógnitas Þ sistema compatible determinado
rg(A) = rg(A*) < nº incógnitas Þ sistema compatible indeterminado¨
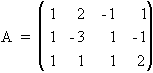
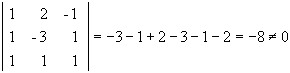
La matriz ampliada será:
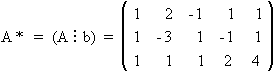
Se puede resolver aplicando la Regla de Cramer, tras adaptar el sistema para tratarlo como si fuera uno de Cramer. Para esto se pasan (n- rg(A)) variables al segundo término, dándole, a partir de entonces, al segundo término el tratamiento de "término independiente" para aplicar la Regla de Cramer.
Como n=4 y rg(A)=3 hay que pasar una variable al segundo término, por ejemplo, x4 . De esta manera las otras tres variables tomarán valores en función de los que tome x4 . El sistema queda como sigue :
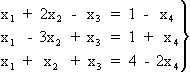
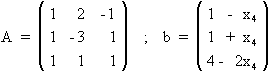
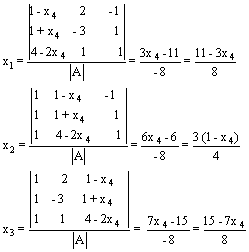
7.- Como ya se ha visto en el ejercicio anterior, discutir un sistema consiste en determinar si tiene o no solución, es decir, si es compatible o incompatible, y en el caso de que tenga solución, determinar si ésta es única (sist. compatible determinado) o si tiene infinitas soluciones (sist. compatible indeterminado). El Teorema de Rouché-Frobenius permite saber si el sistema tiene o no solución, y si la tiene si es única o existen infinitas soluciones. El Teorema se basa en la comparación de los rangos de la matriz A (matriz de coeficientes del sistema de ecuaciones), y la matriz A* (matriz de coeficientes del sistema ampliada con el vector columna de términos independientes del mismo).
La matriz de coeficientes de este ejercicio es
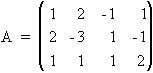
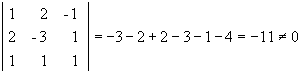
La matriz ampliada es:
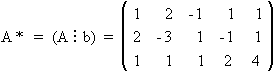
Se puede resolver aplicando la Regla de Cramer, tras adaptar el sistema para tratarlo como si fuera uno de Cramer como en el problema anterior. Como n=4 y rg(A)=3 hay que pasar una variable al segundo término, por ejemplo, x4 . De esta manera las otras tres variables tomarán valores en función de los que tome x4 . El sistema queda como sigue :
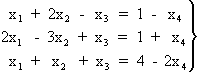
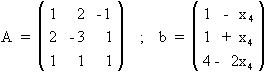
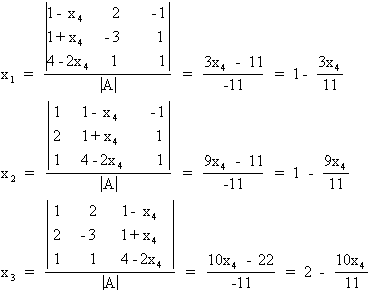
8.-
a)
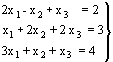
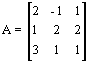
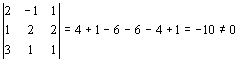
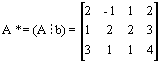
Se puede resolver aplicando la Regla de Cramer. Matricialmente, al tratarse de un sistema de ecuaciones cuadrado, se tiene que
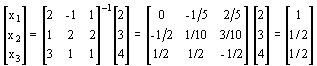
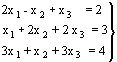
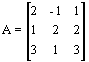
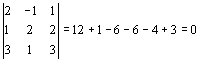
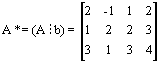
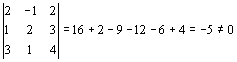
No hay comentarios:
Publicar un comentario